Deques, Priority Queues

 

Deque Data Structure

Deque or Double Ended Queue is a type of queue in which insertion and removal of elements can either be performed from the front or the rear. Thus, it does not follow FIFO rule (First In First Out).

Representation of Deque

---

Types of Deque

• Input Restricted Deque
  In this deque, input is restricted at a single end but allows deletion at both the ends.
• Output Restricted Deque
  In this deque, output is restricted at a single end but allows insertion at both the ends.

---

Operations on a Deque

Below is the circular array implementation of deque. In a circular array, if the array is full, we start from the beginning.

But in a linear array implementation, if the array is full, no more elements can be inserted. In each of the operations below, if the array is full, "overflow message" is thrown.

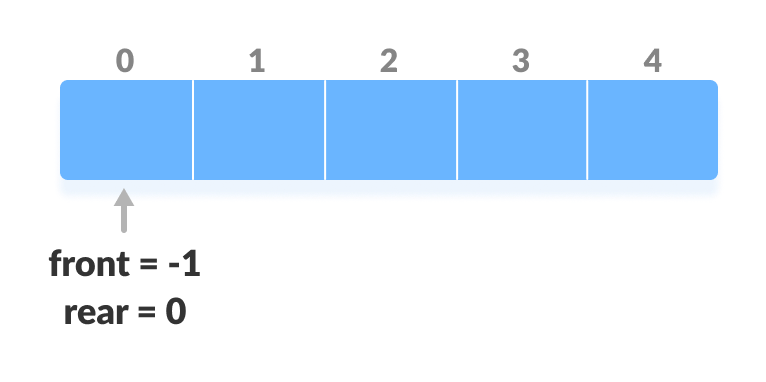
Before performing the following operations, these steps are followed.

1. Take an array (deque) of size n.
2. Set two pointers at the first position and set front = -1 and rear = 0.

Initialize an array and pointers for deque

1. Insert at the Front

This operation adds an element at the front.

1. Check the position of front.

   

   Check the position of front

2. If front < 1, reinitialize front = n-1 (last index).

   

   Shift front to the end

3. Else, decrease front by 1.
4. Add the new key 5 into array[front].

   

   Insert the element at Front

2. Insert at the Rear

This operation adds an element to the rear.

1. Check if the array is full.

   

   Check if deque is full

2. If the deque is full, reinitialize rear = 0.
3. Else, increase rear by 1.

   

   Increase the rear

4. Add the new key 5 into array[rear].

   

   Insert the element at rear

3. Delete from the Front

Priority Queue

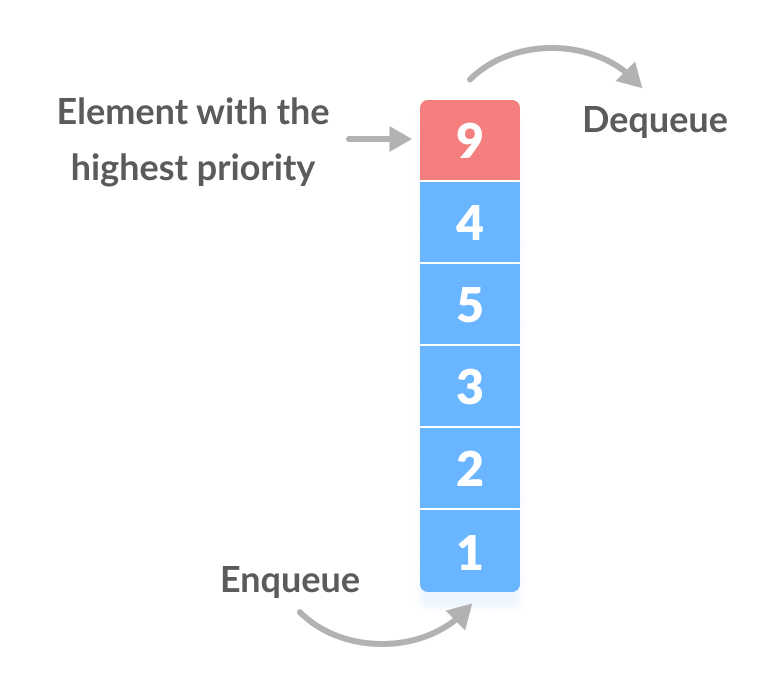
A priority queue is a special type of queue in which each element is associated with a priority value. And, elements are served on the basis of their priority. That is, higher priority elements are served first.

However, if elements with the same priority occur, they are served according to their order in the queue.

Assigning Priority Value

Generally, the value of the element itself is considered for assigning the priority. For example,

The element with the highest value is considered the highest priority element. However, in other cases, we can assume the element with the lowest value as the highest priority element.

We can also set priorities according to our needs.

Removing Highest Priority Element

---

Priority Queue Operations

Basic operations of a priority queue are inserting, removing, and peeking elements.

1. Inserting an Element into the Priority Queue

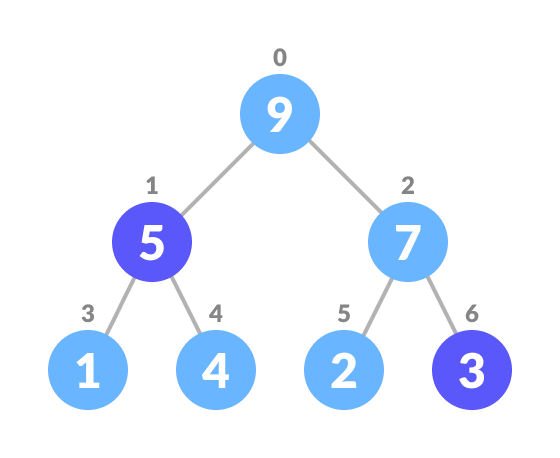
Inserting an element into a priority queue (max-heap) is done by the following steps.

• Insert the new element at the end of the tree.

  

  Insert an element at the end of the queue

• Heapify the tree.

  

  Heapify after insertion

Algorithm for insertion of an element into priority queue (max-heap)

If there is no node, 
  create a newNode.
else (a node is already present)
  insert the newNode at the end (last node from left to right.)
  
heapify the array

For Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.

---

2. Deleting an Element from the Priority Queue

Deleting an element from a priority queue (max-heap) is done as follows:

• Select the element to be deleted.

  

  Select the element to be deleted

• Swap it with the last element.

  

  Swap with the last leaf node element

• Remove the last element.

  

  Remove the last element leaf

• Heapify the tree.

  

  Heapify the priority queue