Counting Number of Binary Trees, Applications of Binary Tree.

 

Given the root of a Complete Binary Tree consisting of N nodes, the task is to find the total number of nodes in the given Binary Tree.

he common non-linear data structure known as a tree. A tree illustrates a hierarchical structure in contrast to other data structures such an array, stack, queue, and linked list, which are linear in nature. A tree's ordering information is irrelevant. Two pointers and nodes make up a tree. The parent node's left and right children are represented by these two pointers. Let's thoroughly comprehend the words used in trees.

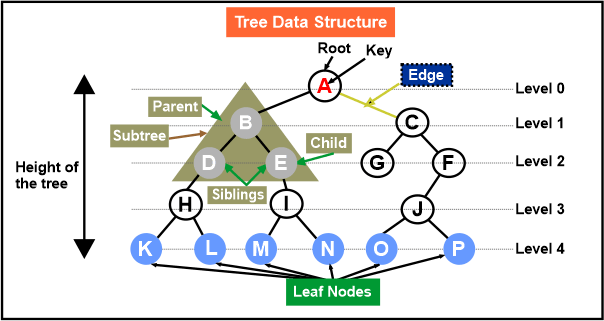
• The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
• Parent Node: A node's parent one is the node that came before it in the tree of nodes.
• Child Node: The node that is a node's direct successor is referred to as a node's child node.
• Siblings are the children of the same parent node.
• Edge: Edge serves as a connecting node between the parent and child nodes.
• Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
• A node's subtree is the tree that views that specific node as the root node.
• Depth: The depth of a node is the separation between it and the root node.
• Height: The height of a node is the distance between it and the subtree's deepest node.
• The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
• Level: In the tree, a level is the number of parents that correspond to a particular node.
• Node degree: A node's degree is determined by how many children it has.
• A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.